Avtor slike: Teja Rutar

Naloga 1

Naredi seznam poljubnih števil. Z uporabo zank izpiši:

• vsa števila v seznamu (vsakega v svoji vrstici),
• vsa števila v obratnem vrstnem redu,
• kvadrat vsakega števila,
• vsa števila, ki so večja od 5,
• vsa števila, ki so večja od 5 in manjša od 10,
• največje število,
• najmanjše število,
• vsoto vseh števil,
• vsa števila, ki so večja od prejšnjega števila,
• seznam urejen od najmanjšega do največjega števila (težje).

Naloga 2

Izpiši števila od 1 do 100. Če je število deljivo s 3 izpiši Fizz, če je deljivo s 5 Buzz, če je deljivo s 3 in 5 pa FizzBuzz.

Naloga 3

Izpiši sledeči vzorec:

*
**
***
****
*****

Velikost naj bo zapisana v spremenljivki velikost. Zgornji primer je za velikost = 5.

Podobno nariši tudi smrekico:

    *
   ***
  *****
 *******
*********

Naloga 4

Izpiši prvih 100 Fibonaccijevih števil. Fibonaccijeva števila se začnejo z 0 in 1, vsako naslednje število pa je vsota prejšnjih dveh:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

Naloga 5

Izpiši vse praštevila do 1000. Praštevila so števila, ki so deljiva samo z 1 in samim seboj.

Naloga 6

Izpiši tabelo množenja za poljubno število. BONUS: Presledki naj bodo prilagojeni številu, da bo tabela lepa.

Primer za 5:

1  2  3  4  5
2  4  6  8 10
3  6  9 12 15
4  8 12 16 20
5 10 15 20 25

---

Naloga 7

Izračunajte število kock, ki jih potrebujemo, da sestavimo stolp višine h.
Stolp na skici ima višino h = 4.

• Poskusite svoj program optimizirati.
• Se ga da napisat v eni sami vrstici?

Naloga 8

Imamo celi števili A in B.
Napišite funkcijo deljivost(a, b):, ki pove koliko številk na intervalu [1, 1000] je deljivih z a in ne z b.

Naloga 9

Napišite funkcijo tekme(ekipe), ki za vhodni parameter vzame nabor ekip, ter vrne vse tekme tako, da bo vsaka ekipa igrala z vsako drugo.

primer:
ekipe = ["tolmin", "kamno", "zatmin"]

izpis:

tolmin VS kamno
tolmin VS zatmin
kamno VS zatmin

naloga 10 (4 letnik)

Napišite funkcijo za nnumerično integracijo 🙂🙂🙂.

Razlaga

Stvar ni tako zakomplicirana, če vemo, da določeni integral izračuna ploščino grafa pod krivuljo.

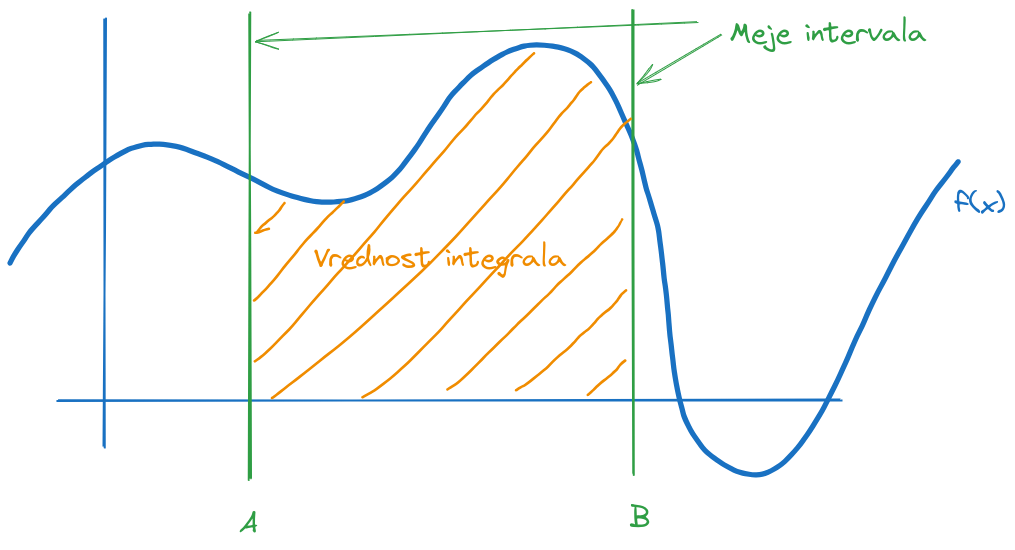
Ker so integrali zahtevni za računat, lahko vrednost določenega integrala aproksimiramo (določimo približek) z naslednjo metodo.

Območje razdelimo na enako široke stolpce, z višino y = f(x). Ploščina stolpca pa je enostavna. S = y * dx, kjer je dx standardna oznaka za širino stolpca.

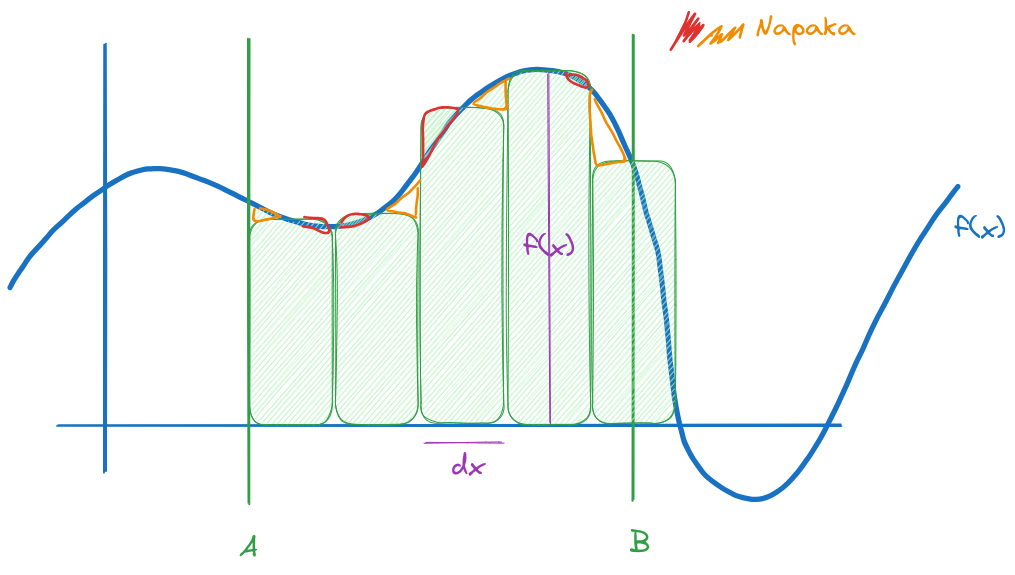
Ploščino pod krivuljo dobimo tako, da seštejemo vse površine stolpcev.

Stolpce ustvarimo tako, da se sprehodimo z zanko od začetka do konca intervala. namig: range(a, b, dx)

Opazimo, da se stolpci ne prilegajo krivulji perfektno. Z rdečo in oranžno je označena napaka.
Če želimo napako zmanjšati, zmanjšamo širino stolpcev (zmanjšamo dx)

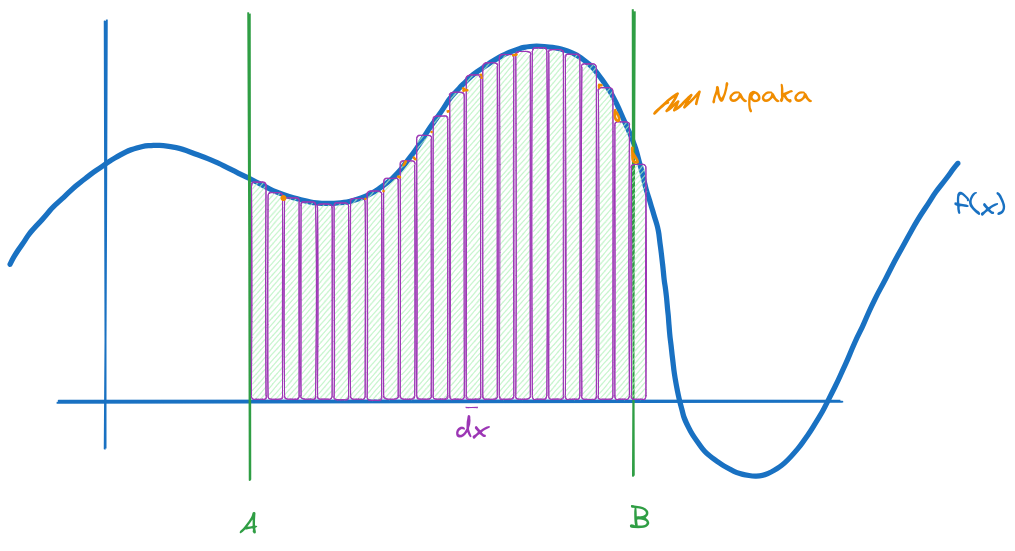
Vijolični stolpci so tako zelo ozki, da se grafu že skoraj popolnoma prilegajo, seštevek njihovih ploščin pa je že zelo blizu vrednosti integrala.

Naloga

napišite funkcijo num_int(f, a, b), ki sprejme za parametre realni števili a,b ter funkcijo f(x).

Poskusite integrirati kvadratno funkcijo xˇ2 na intervalu -2, 3.

# kvadratna funkcija
def f(x):
    return x * x